참고문헌 :
https://ko.wikipedia.org/wiki/%ED%8A%B8%EB%A6%AC_%EA%B5%AC%EC%A1%B0
트리 구조 - 위키백과, 우리 모두의 백과사전
위키백과, 우리 모두의 백과사전.
ko.wikipedia.org
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
[자료구조] 트리(Tree)란 - Heee's Development Blog
Step by step goes a long way.
gmlwjd9405.github.io
트리의 종류와 이해
트리의 종류와 이해 0. 목차 목차 tree란? tree의 종류 결론 참고자료 1. tree란? tree 자료구조는 그래프의 한 종류로, 정의 내리자면 트리란 어떤 노드들의 집합으로 노드들은 각 서로 다른 자식을 가
www.secmem.org
1. 트리 정의
- 그래프의 한 종류로 루트 노드(root node, 최상위 노드)가 0개 이상의 노드(자식 노드)를 가지고 또 그 자식 노드가 0개 이상의 노드를 가지는 것을 의미합니다.
- 사이클이 없는 하나의 연결 그래프입니다.

2. 트리 용어 정리
1) root node : 부모 노드가 없고 자식 노드만 가지는 노드. (예시 1에서는 node a 가 해당됩니다.)
2) leaf node : 자식 노드가 없는 노드. (예시 1에서는 node b, node d, node e 가 해당됩니다.)
3) depth : root node에서 특정 노드로 이동할 때 거쳐야 하는 간선의 수. (예시 1에서는 node e의 depth는 2가 됩니다.)
4) level : 같은 깊이를 가지는 노드의 집합. (예시 1에서는 level 0의 집합은 a이고 level 1의 집합은 b, c, d가 됩니다.)
5) height : 깊이가 가장 큰 값이 트리의 높이가 됩니다. (예시 1의 height는 2가 되겠습니다.)
3. 트리 종류 (이진트리)
- 트리의 종류로는 아주 다양합니다. AVL트리, 레드-블랙 트리 등등 종류가 많은 데 해당 글에서는 이진트리에 대하여 만 다루도록 하겠습니다.
1. 이진트리 정의
- 각 노드가 최대 2개의 자식 노드를 가지는 트리를 의미합니다. <트리 예시 2>가 이진트리에 속해있다고 할 수 있습니다.
2. 이진트리 종류
- 완전 이진트리 (Complete Binary Tree) : 왼쪽 자식부터 가지며 마지막 레벨을 제외하고 모든 레벨은 완전치 채워져 있습니다.

설명 :
2)가 완전 이진트리가 아닌 이유는 마지막 레벨은 2인데 레벨 1이 완전히 채워져 있지가 안기 때문입니다.
3)가 완전 이진트리가 아닌 이유는 왼쪽 자식부터 순차적으로 가지는 node b를 보면 왼쪽 자식은 없는데 오른쪽 자식이 있기 때문입니다.
- 포화 이진트리 (Perfect Binary Tree) : 모든 노드가 0개 또는 2개의 자식을 가지고 있으며 leaf node들의 depth는 동일해야 합니다.

설명 :
오른쪽 트리가 포화 이진트리가 아닌 이유는 leaf 노드는 c, d, e인데 c의 depth는 1이고 나머지는 depth 2로 모두 동일한 depth가 아니므로 포화 이진트리가 아닙니다.
- 전 이진트리 (Full Binary Tree) : 모든 노드가 0 또는 2개의 자식 노드를 가지는 것을 말합니다.

설명 :
왼쪽 트리가 전 이진트리가 아닌 이유는 node a의 자식이 하나만 있기 때문입니다.
3. 이진트리 탐색
- 전위 순회(pre-order traversal) : 현재 노드 -> 왼쪽 자식 노드 -> 오른쪽 자식 노드


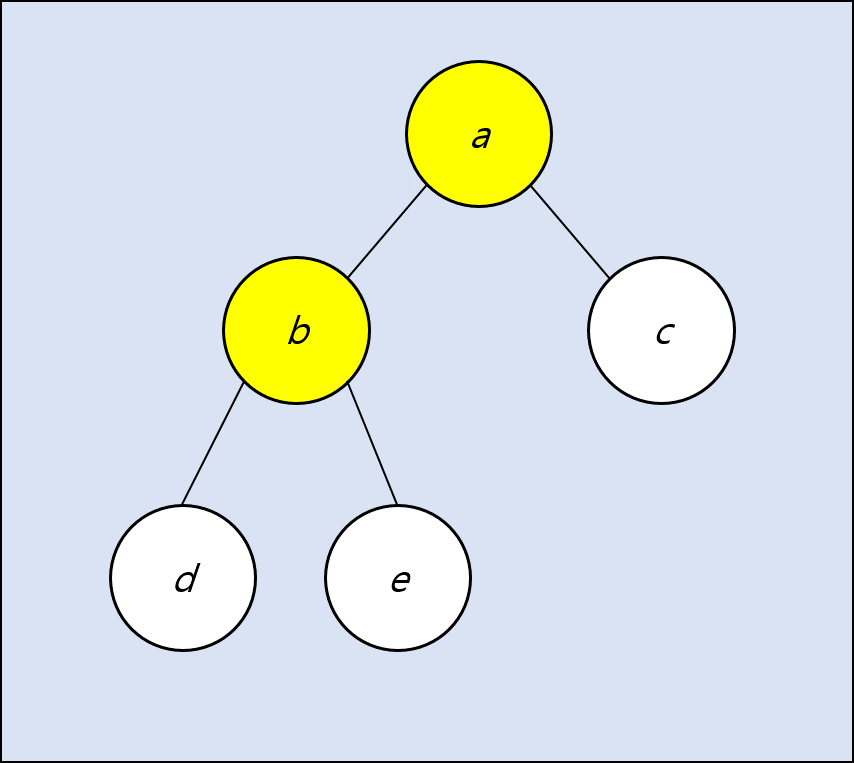



방문 순서 : a -> b -> d -> e -> c
- 중위 순회 (in-order traversal) : 왼쪽 자식 노드 -> 현재 노드 -> 오른쪽 자식 노드



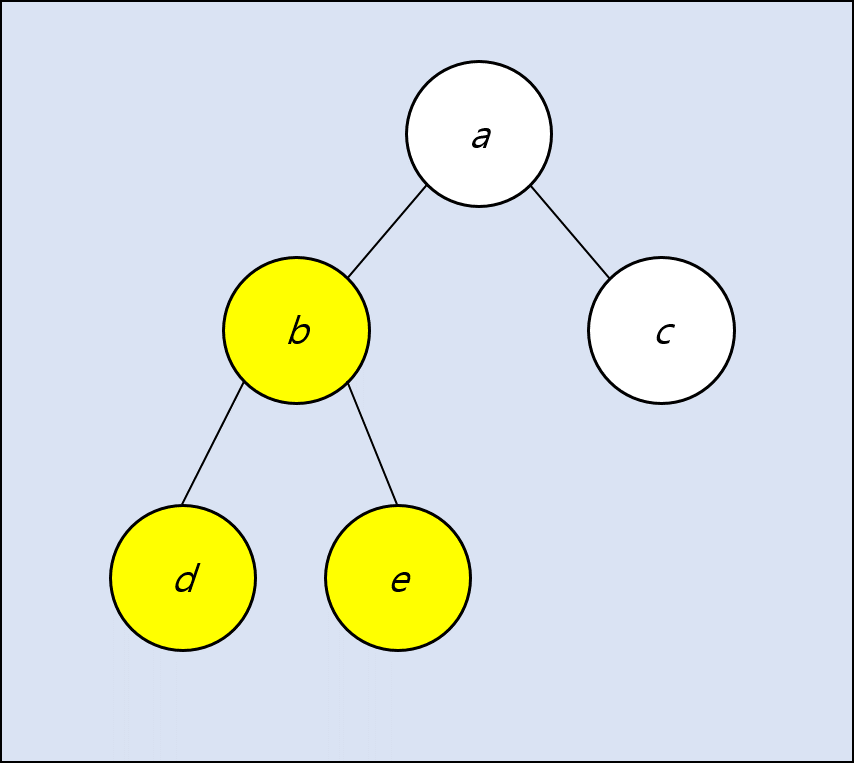


방문 순서 : d -> b -> e -> a -> c
- 후위 순회 (post-order traversal) : 왼쪽 자식 노드 -> 오른쪽 자식 노드 -> 현재 노드






방문 순서 : d -> e -> b -> c -> a
4. 노드 순회 코드 (아주 간단)
typedef struct myNode{
char name[10];
struct myNode *leftNode;
struct myNode *rightNode;
} node;
/* 전위 순회 */
void pre_order(node * root) {
if(root != null){
printf("%s ", root->name);
pre_order(root->leftNode);
pre_order(root->rightNode);
}
}
/* 중위 순회 */
void in_order(node * root) {
if(root != null) {
in_order(root->leftNode);
print("%s ", root->name);
in_order(root->rightNode);
}
}
/* 후위 순회 */
void post_order(node * root) {
if(root != null) {
post_order(root->leftNode);
post_order(root->rightNode);
printf("%s ", root->name);
}
}'개념 정리 > 자료구조' 카테고리의 다른 글
| 자료구조 : 그래프 (0) | 2021.05.05 |
|---|---|
| 자료구조 : 링크드 리스트 (0) | 2021.04.28 |
| 자료구조 : 덱 (0) | 2021.03.08 |
| 자료구조 : 힙 (with 우선순위 큐) (0) | 2021.02.22 |
| 자료구조 : 큐 (0) | 2021.02.21 |

