자료구조 : 힙 (with 우선순위 큐)

참고 문헌 :

codingdog.tistory.com/entry/%EC%99%84%EC%A0%84%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%AC-vs-%ED%8F%AC%ED%99%94%EC%9D%B4%EC%A7%84%ED%8A%B8%EB%A6%AC-%EC%9D%B4-%EB%91%98%EC%97%90-%EB%8C%80%ED%95%B4-%EC%95%8C%EC%95%84%EB%B4%85%EC%8B%9C%EB%8B%A4

완전이진트리 vs 포화이진트리 : 이 둘에 대해 알아봅시다.

 

velog.io/@holicme7/%EC%9A%B0%EC%84%A0%EC%88%9C%EC%9C%84-%ED%81%90Prioirity-Queue-mbk48cz764

우선순위 큐(Prioirity Queue) (1) - 최대 힙 이용

 

gmlwjd9405.github.io/2018/05/10/data-structure-heap.html

[자료구조] 힙(heap)이란 - Heee's Development Blog

 

chanhuiseok.github.io/posts/ds-4/

자료구조 - 우선순위 큐(Priority Queue)와 힙(heap)

---

1. 힙 (Heap)

1.1 정의 : 완전 이진트리 구조를 가지며 모든 노드에 저장되는 값은 자식 노드에 저장되는 값 보다 우선순위가 높습니다.

 

1.2 종류 : 

   1) 최대 힙 (Max Heap) : 모든 부모 노드가 자식 노드보다 크거나 같을 때를 의미합니다.

   2) 최소 힙 (Min Heap) : 모든 부모 노드가 자식 노드보다 작거나 같을 때를 의미합니다.

< 최대힙 상태 >

 

< 최소힙 상태 >

---

2. 힙 구현하기 (최대 힙 기준 설명, 최소 힙은 반대로 생각하면 됩니다.)

0. 부모 노드와 자식 노드 관의 관계

 

시작 index = 0 일 때

< 시작 index = 0 일 때 >

부모 노드 -> 왼쪽 자식 노드 : 자신 index * 2 + 1

부모 노드 -> 오른쪽 자식 노드 : ( 자신 index + 1 ) * 2

자식 노드 -> 부모 노드 : (자신 index - 1) / 2

 

시작 index = 1일 때 

< 시작 index = 1 일 때 >

부모 노드 -> 왼쪽 자식 노드 : 자신의 index * 2

부모 노드 -> 오른쪽 자식 노드  자신의 index * 2 + 1

자식 노드 -> 부모 노드 : 자신의 index / 2

 

*이 처럼 볼 수 있듯이 시작 index가 1이면 계산식이 간단한 대신 index = 0 일 때의 빈 공간이 생기고 시작 index가 0이면 계산식 살짝 복잡해지는 대신에 빈 공간이 생기진 않습니다.

 

1. 힙의 데이터 추가 

 

- 힙에 새로운 데이터가 추가되면 우선 힙의 마지막에 데이터를 추가합니다.

- 부모 노드와 우선순위를 비교하여 힙을 완성시킵니다.

 

힙에 데이터를 추가하는 과정은 다음과 같습니다.

< heap 모습 >

 - 현재 힙 상태에 값이 30인 데이터를 추가하도록 하겠습니다.

 

< 힙에 30 데이터 추가 모습 >

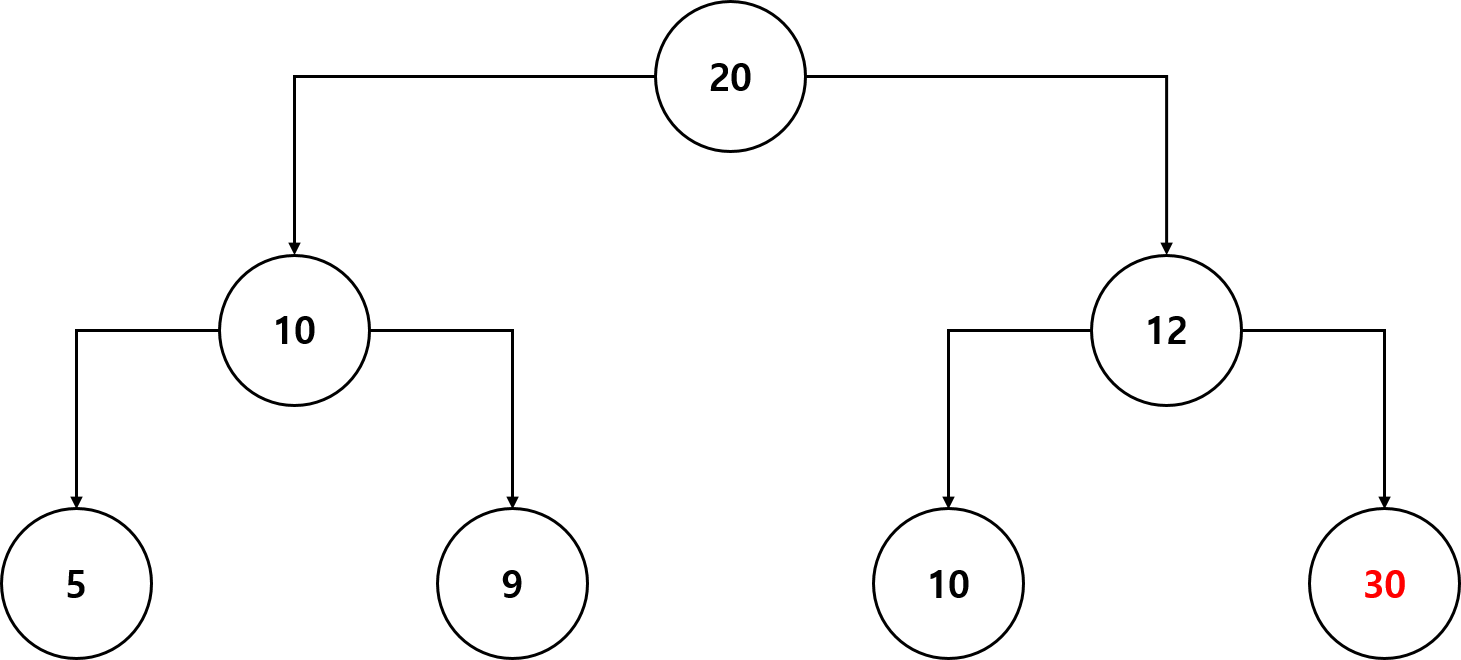
- 이렇게 힙의 끝에 데이터를 추가합니다. 

 

< 부모 노드 보다 우선순위가 높아서 서로 교체 >

- 부모 노드(12)와 비교했을 때 자신의 우선순위가 높으므로 부모 노드와 값을 바꿉니다.

 

< 현재 자신의 부모가 존재하므로 부모 노드과 비교합니다. >

- 현재 자신의 위치가 최상위 아니므로(부모 노드가 존재하므로) 부모 노드와 비교합니다. 부모 노드(20) 보다 자신의 우선순위가 높으므로 부모 노드와 값을 바꿉니다.

- 그리고 현재의 자신의 위치가 최상위 이므로(부모 노드가 존재하지 않으므로) 데이터 추가는 완료됩니다.

 

2. 힙의 데이터 삭제

 

- 최상위에 있는 노드(루트 노드)를 제거합니다.

- 힙의 마지막 노드를 최상위에 있는 노드(루트 노드) 자리로 이동하고 힙을 재구성합니다.

 

힙에 데이터를 삭제하는 과정은 다음과 같습니다.

 

< 힙 상태 >

- 여기서 우선순위가 가장 높은 데이터 (30)을 삭제하겠습니다.

 

< 루트 노드를 삭제 >

- 루트 노드를 삭제합니다. 그리고 가장 마지막 노드인 12를 루트 노드로 이동합니다.

 

< 부모 노드랑 자식 노드랑 비교합니다. >

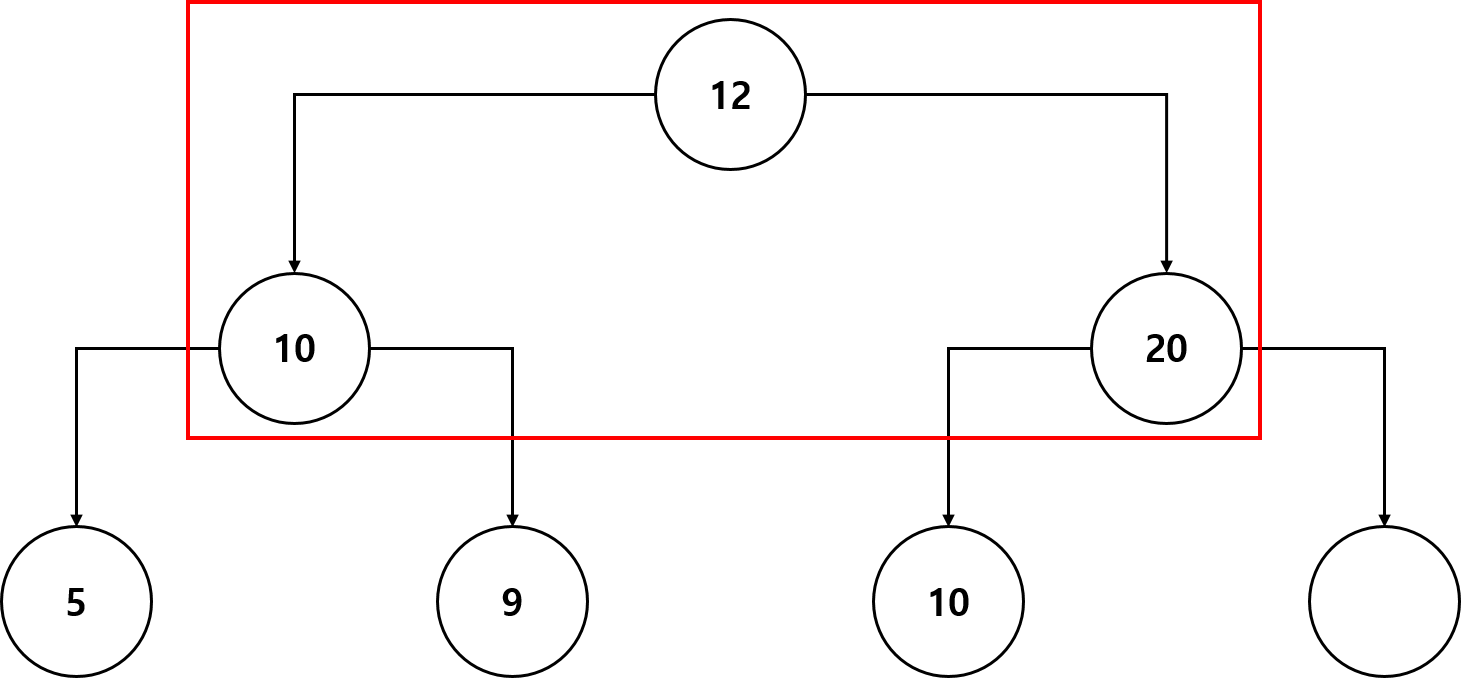
- 부모 노드랑 자식 노드랑 비교하여 최대 힙에 맞는지 확인합니다.

 

< heap 재 구성 >

- 부모 노드보다 오른쪽 자식 노드의 우선순위가 높으므로 둘의 값을 바꿉니다. (현재 상황은 오른쪽 자식 노드만 부모 노드보다 큰 경우인데, 둘 다 부모 노드보다 큰 경우에는 더 큰 우선순위를 가진 자식 노드와 자리를 바꿉니다.

- 자리를 바꾼 후 최대 힙이 구성되었으므로 데이터 삭제는 완료됩니다.

 

힙 구현하기 (최대 힙, C99)

 

#include<stdio.h>

int heap[100];
int index = -1;

void insert(int data)
{
	if(index < 100)
	{
		heap[++index] = data;
		
		int sun = index;
		
		while(sun)
		{
			int parent = (sun - 1) / 2;
			
			if(heap[parent] < heap[sun])
			{
				int tmp = heap[sun];
				heap[sun] = heap[parent];
				heap[parent] = tmp;
				sun = parent;
			}
			else
				sun = 0;
		}
	}
	else
		printf("heap is full!\n");
}

int delete()
{
	if(index > -1)
	{
		int result = heap[0];
		
		heap[0] = heap[index--];
		
		int parent = 0;
		
		while(1)
		{
			int lsun = parent * 2 + 1;
			int rsun = (parent + 1) * 2;
			
			lsun = lsun <= index ? lsun : 0;
			rsun = rsun <= index ? rsun : 0;
			
			if(lsun && rsun)
			{
				if(heap[parent] < heap[lsun] || heap[parent] < heap[rsun])
				{
					int big = heap[rsun] > heap[lsun] ? rsun : lsun;
					int tmp = heap[parent];
					
					heap[parent] = heap[big];
					heap[big] = tmp;
					parent = big;
				}
				else
					break;
			}
			else if(lsun)
			{
				if(heap[parent] < heap[lsun])
				{
					int tmp = heap[parent];
					heap[parent] = heap[lsun];
					heap[lsun] = tmp;
				}
				else
					break;
			}
			else
				break;
		}
		
		return result;
	}
	else
	{
		printf("heap is empty!\n");
		return -1;
	}
}

 

---

3. 우선순위 큐 과 힙의 관계

- 위의 힙의 데이터 추가 및 삭제 과정을 보면 모든 과정이 O(logN)의 시간이 걸립니다.

- 우선순위 큐를 링크드 리스트, 배열로 구현할 때 우선순위에 맞게 데이터를 정렬하는 과정이 필요합니다. 이때 최소의 시간의 O(n)이 되겠습니다.

- 따라서 우선순위 큐를 힙으로 구현하는 것이 가장 효율적입니다.