참고 문헌 :
https://blog.naver.com/ndb796/221234424646
23. 다익스트라(Dijkstra) 알고리즘
다익스트라(Dijkstra) 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로(Shortest Path) 탐...
blog.naver.com
https://hsp1116.tistory.com/42
다익스트라 알고리즘(Dijkstra Algorithm)
그래프에서 정점끼리의 최단 경로를 구하는 문제는 여러가지 방법이 있다. 하나의 정점에서 다른 하나의 정점까지의 최단 경로를 구하는 문제(single source and single destination shortest path problem) 하.
hsp1116.tistory.com
데이크스트라 알고리즘 - 위키백과, 우리 모두의 백과사전
컴퓨터 과학에서, 데이크스트라 알고리즘(영어: Dijkstra algorithm) 또는 다익스트라 알고리즘은 도로 교통망 같은 곳에서 나타날 수 있는 그래프에서 꼭짓점 간의 최단 경로를 찾는 알고리즘이다.
ko.wikipedia.org
1. 다익스트라 알고리즘 개념 정리
- 그래프의 특정 노드에서 시작하여 그래프의 모든 노드로 가는 최단 경로를 구하는 알고리즘입니다.
- 그래프의 가중치가 음수인 간선이 없는 경우에만 사용할 수 있습니다.
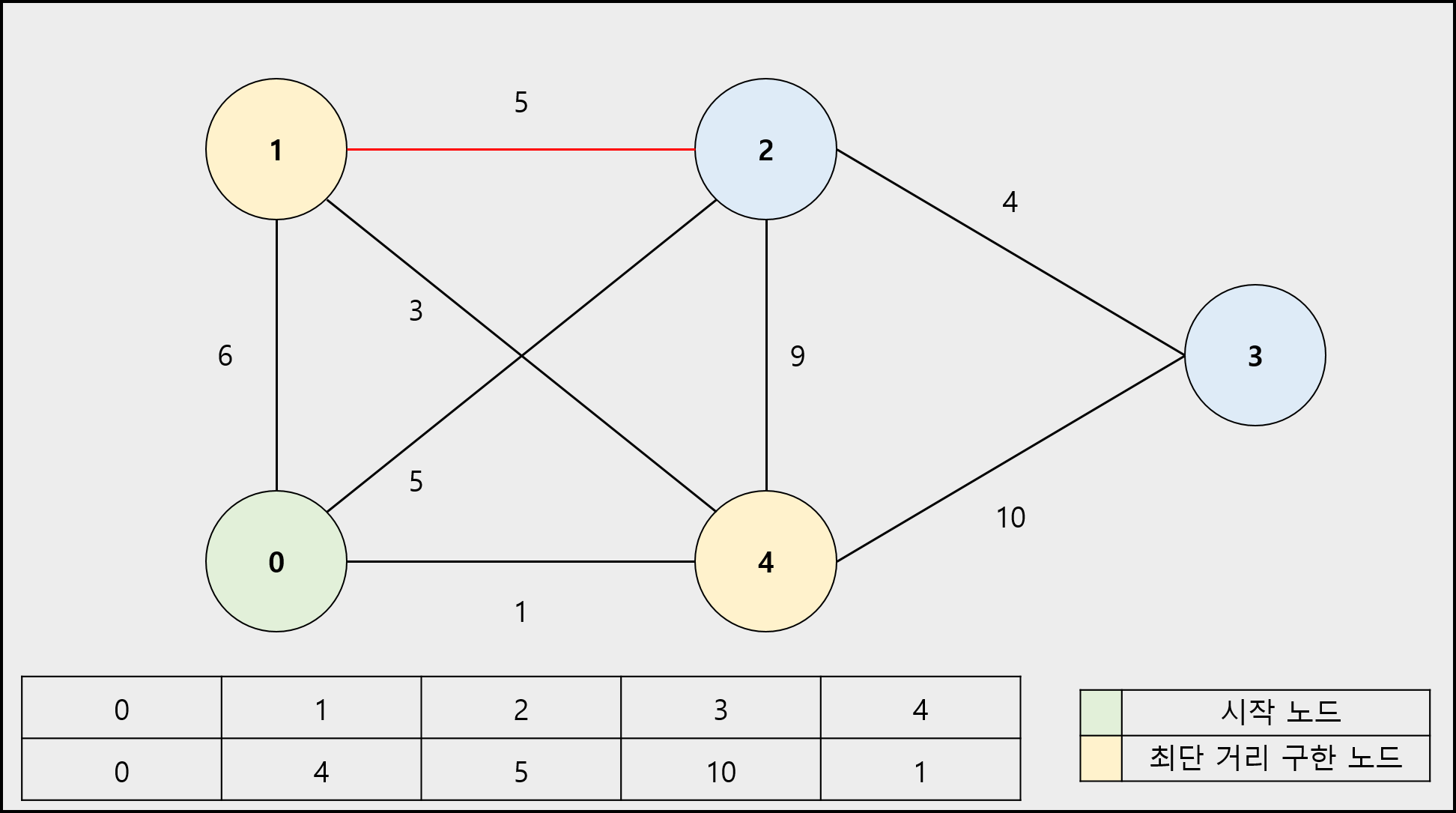
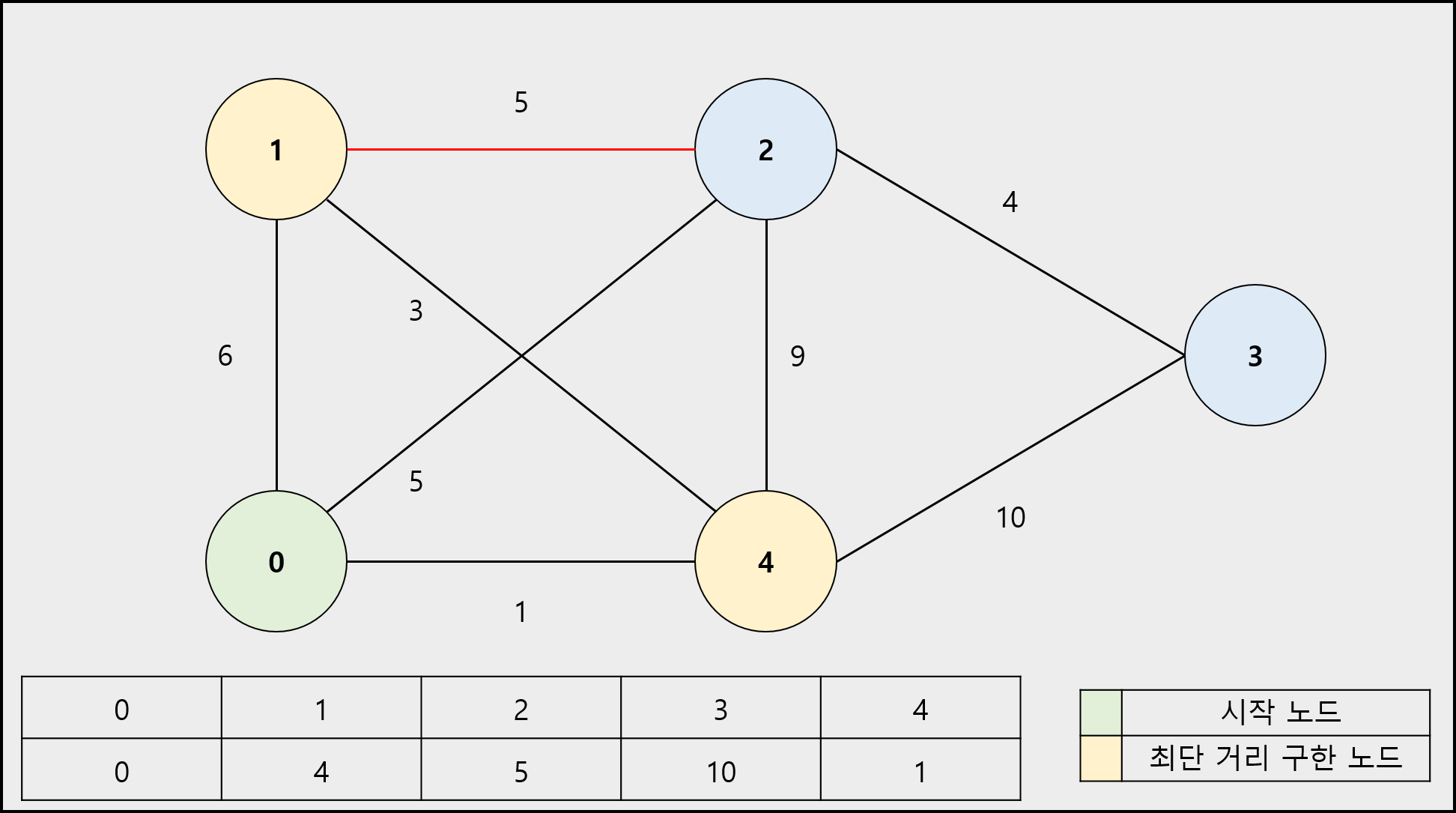
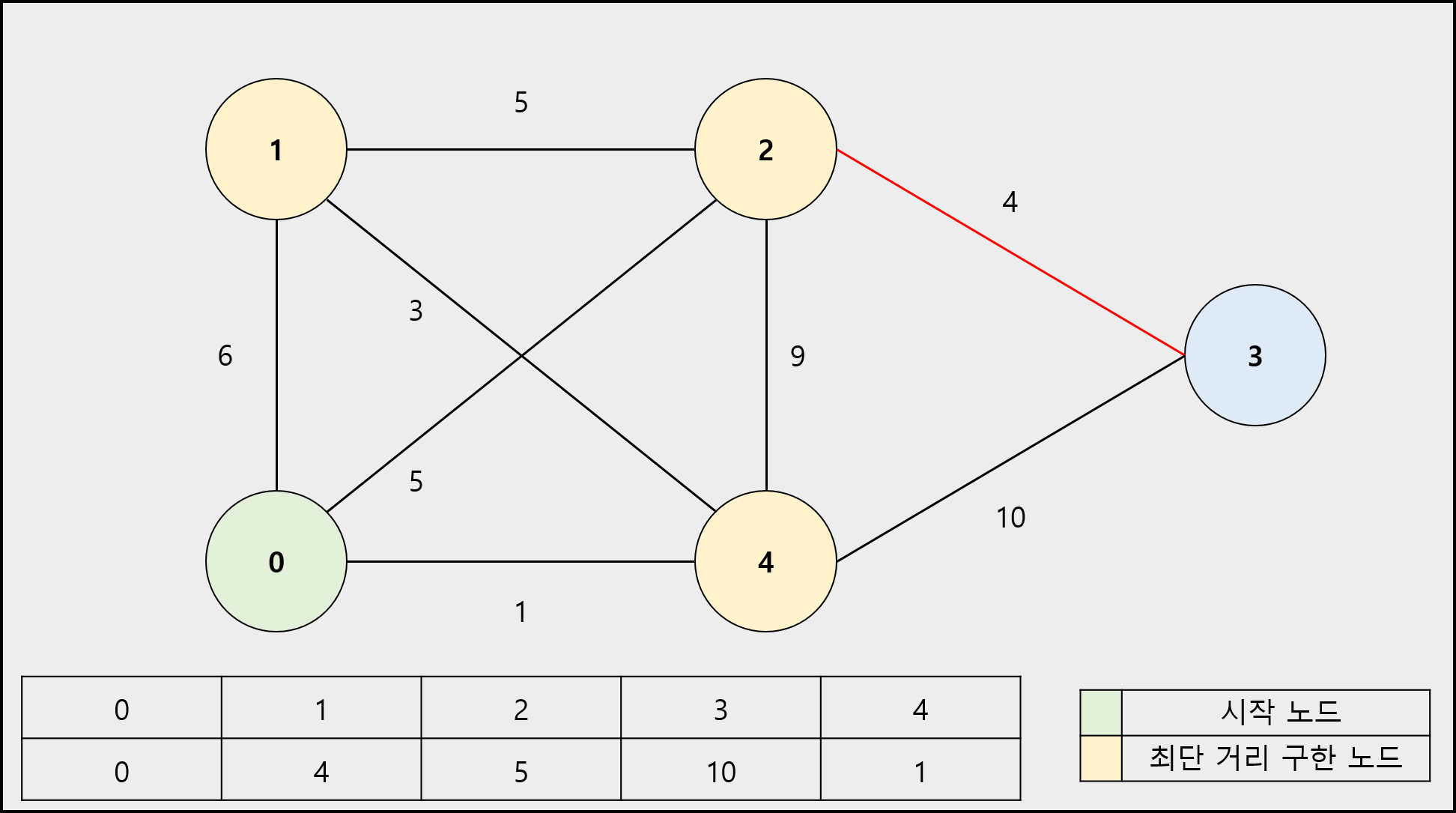
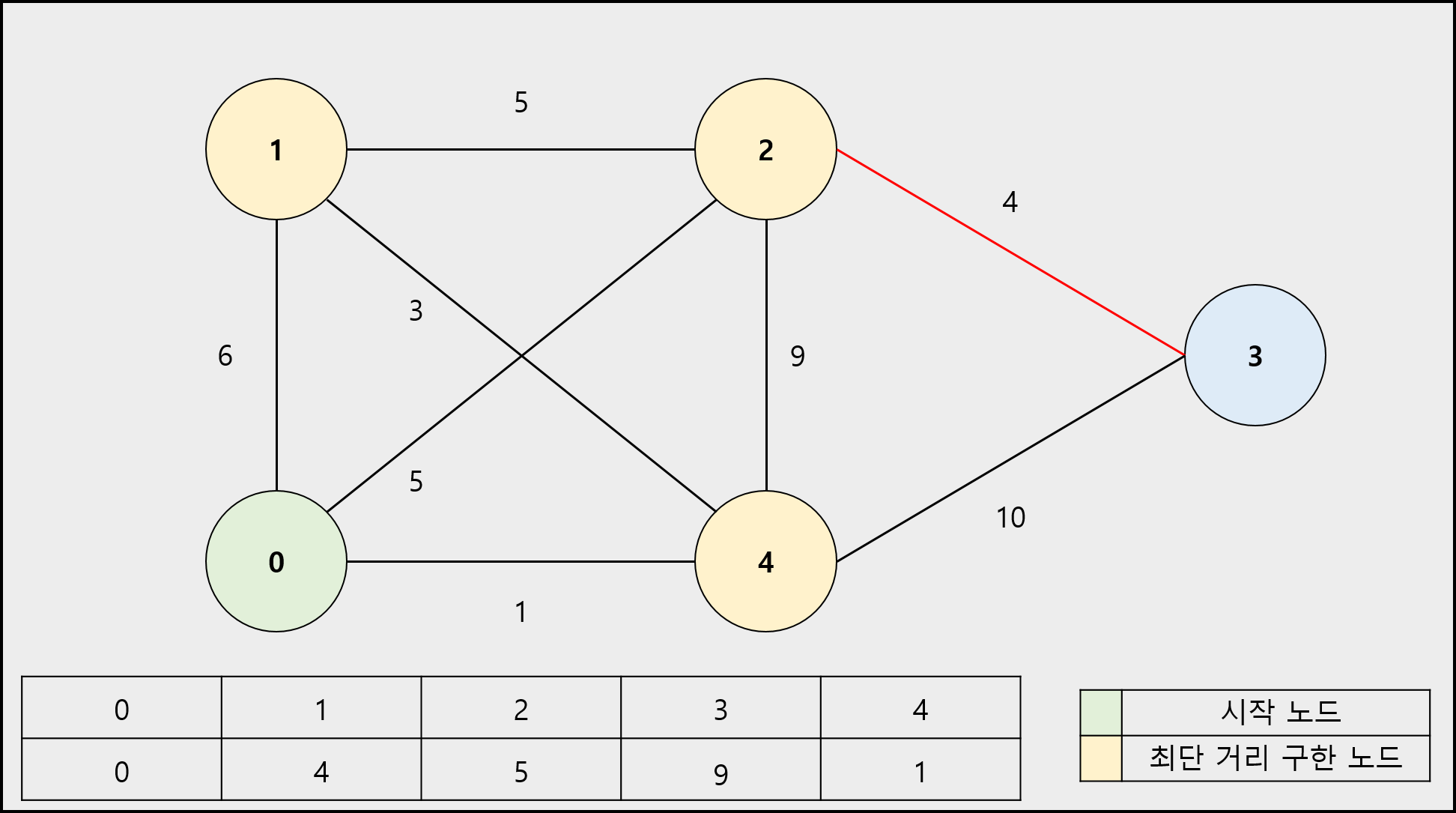
알고리즘 진행 과정
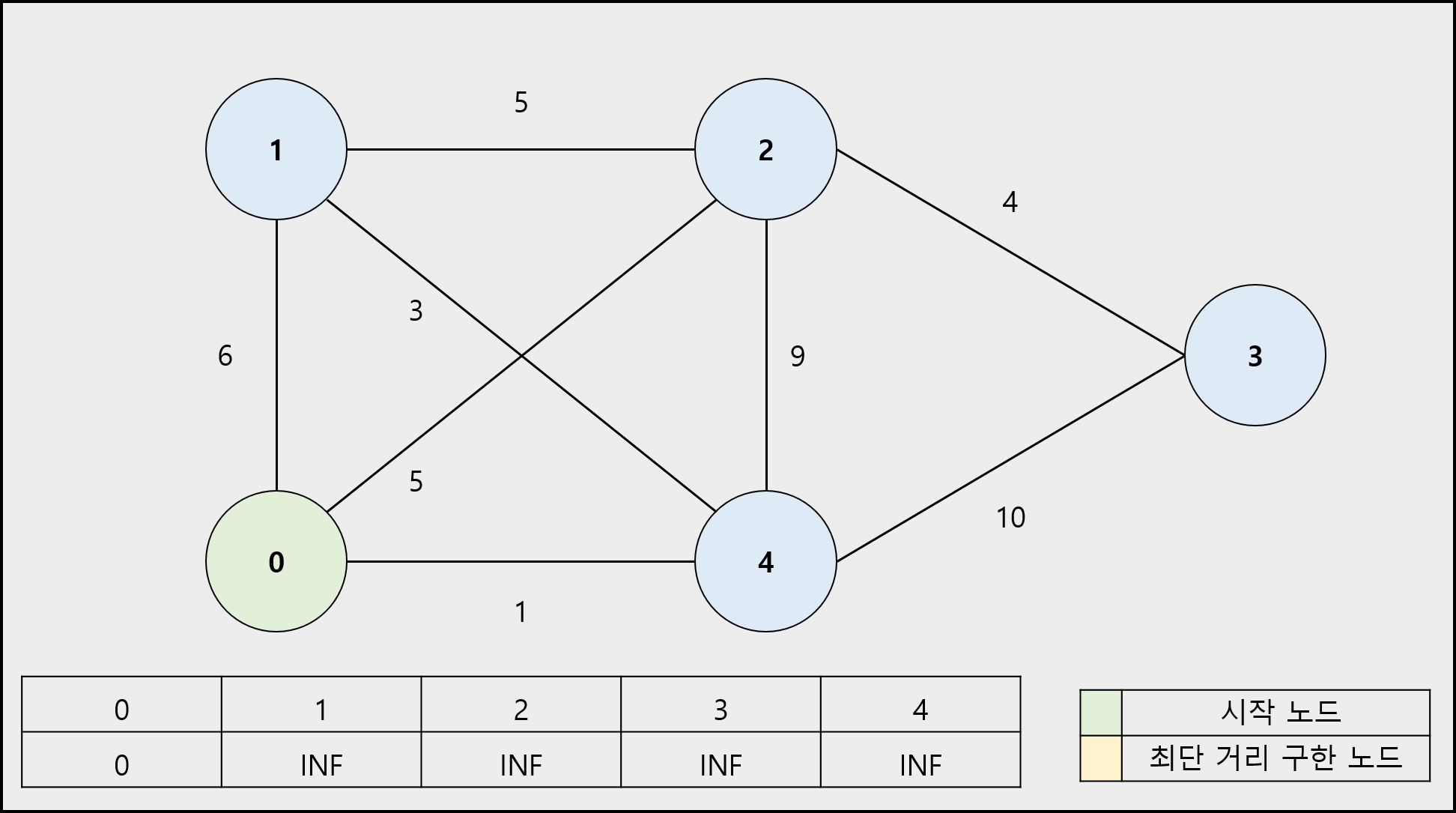
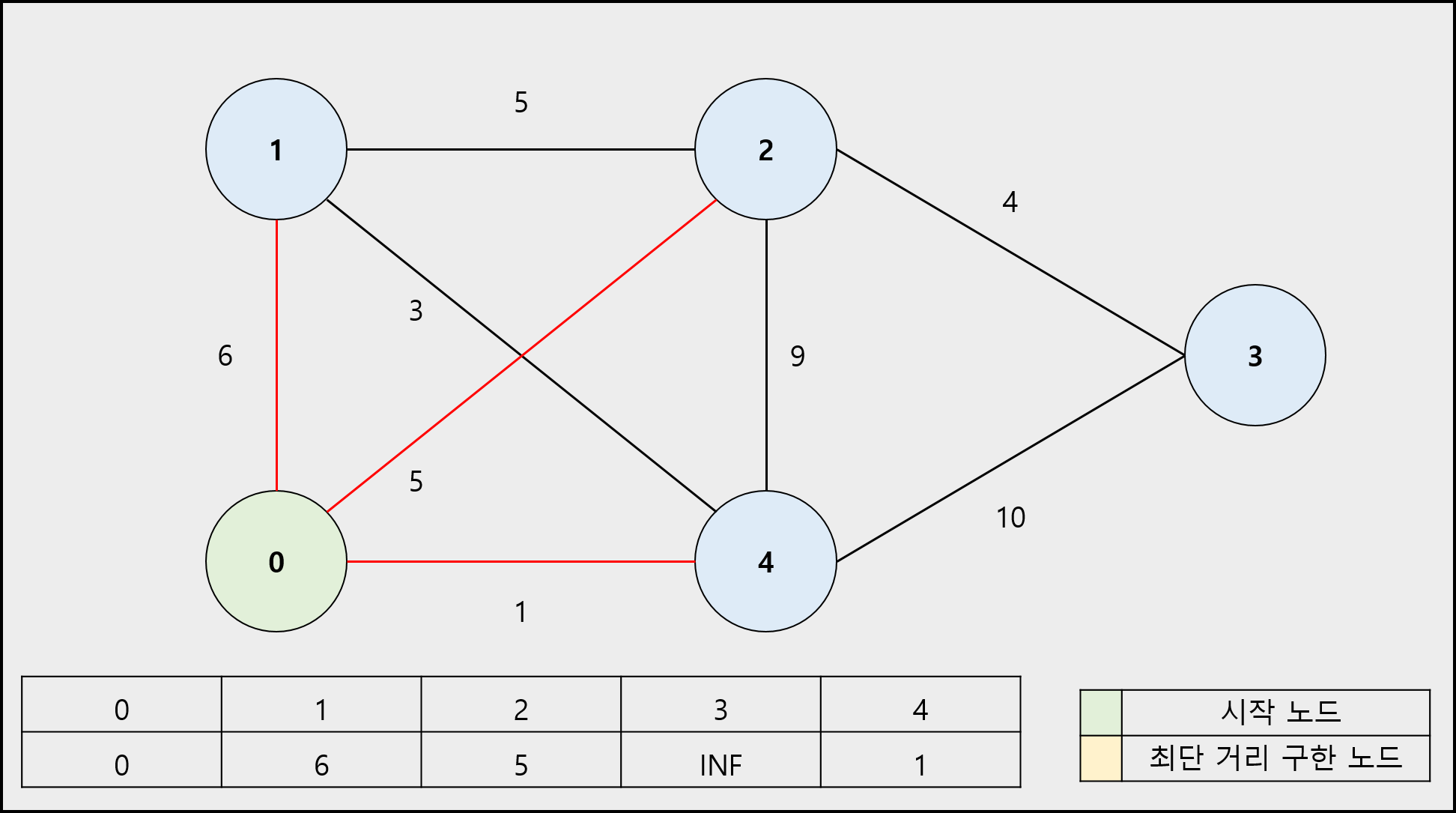
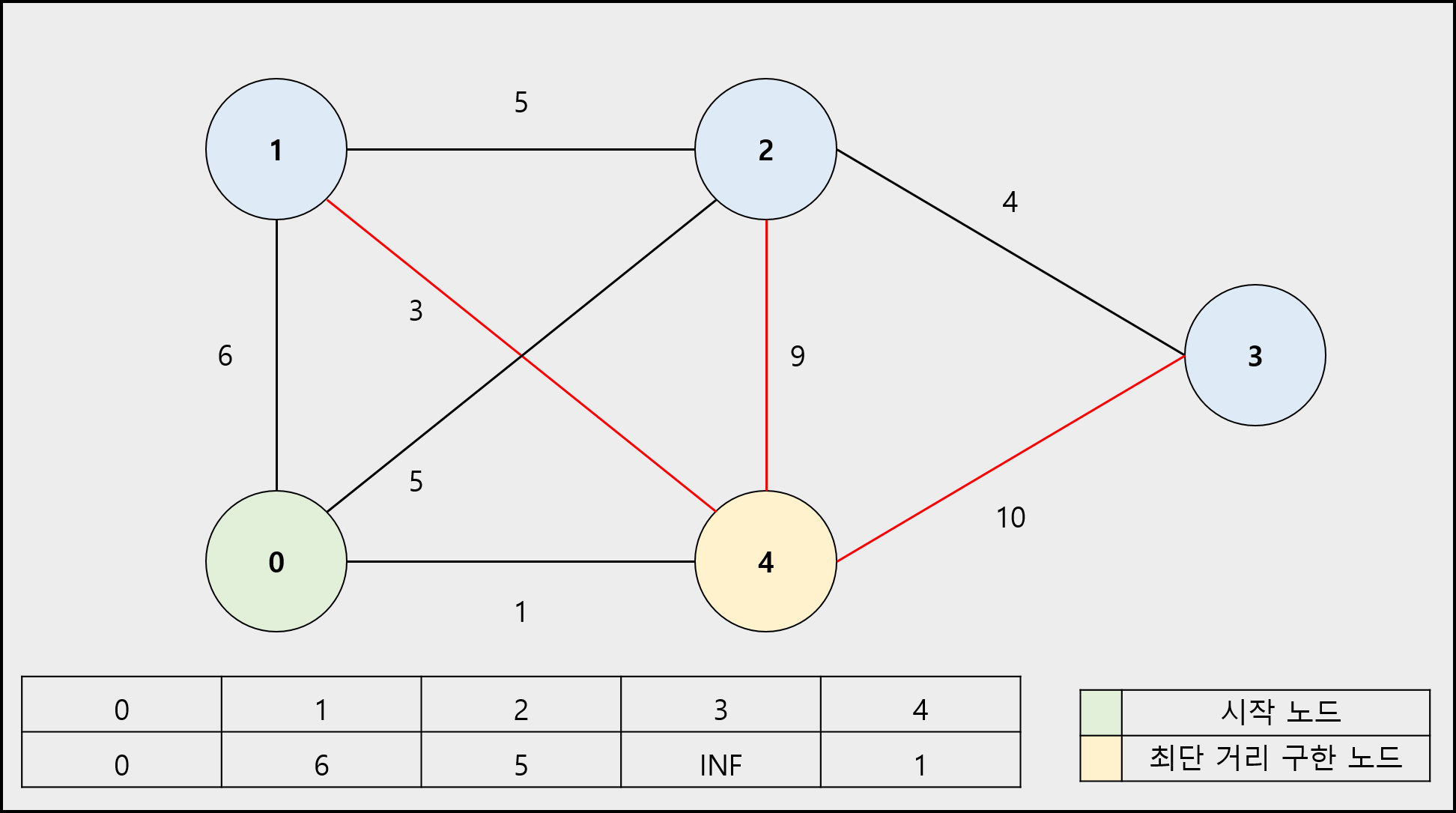
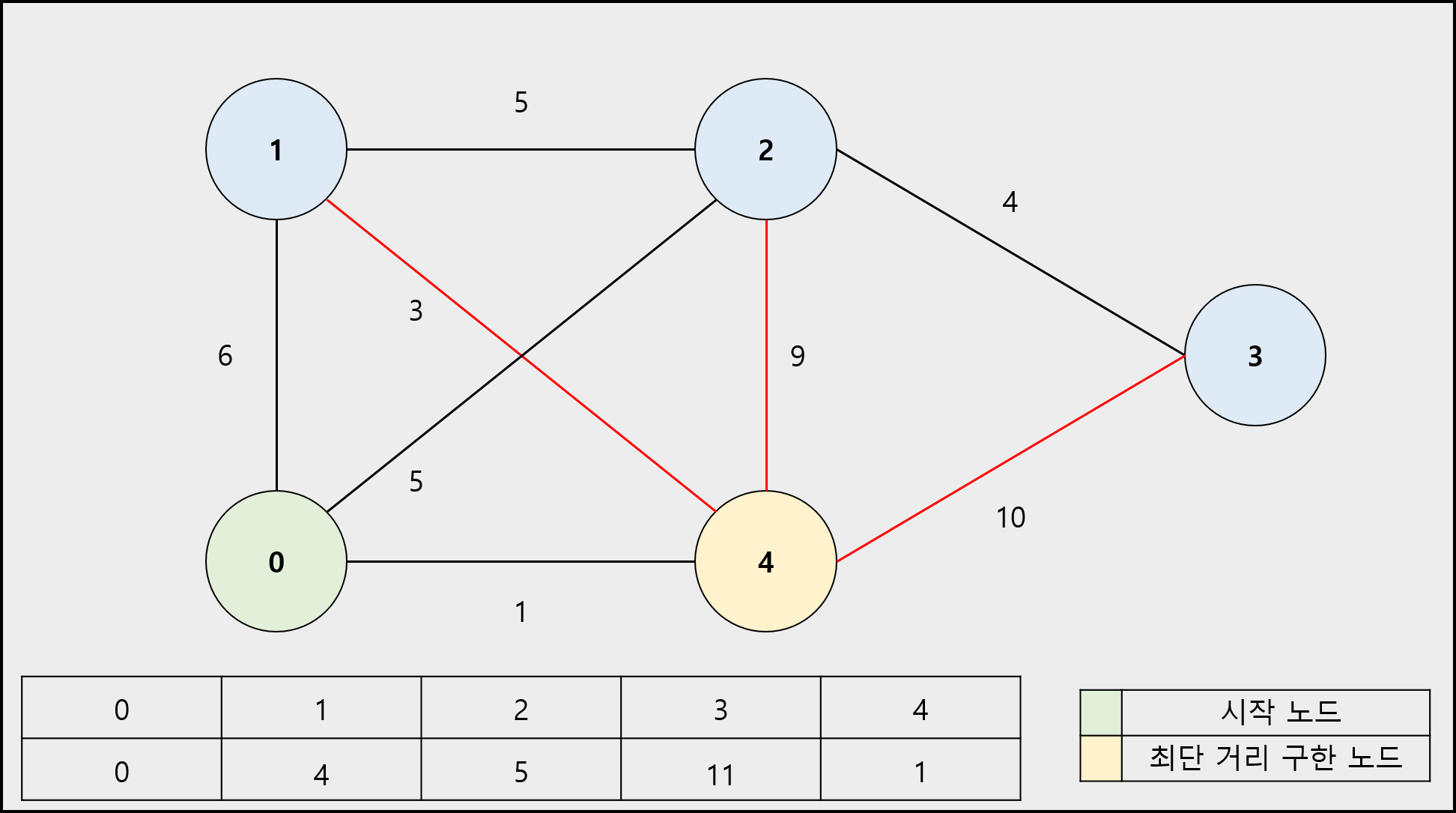
1) 시작 노드의 이동 거리는 0으로 나머지 정점의 이동 거리는 무한(INF)으로 초기화합니다. (시작 노드는 최단 거리를 구한 노드로 설정합니다.)
2) 시작 노드의 인접 노드의 이동 거리를 간선의 가중치로 바꿉니다.
3) 최단 거리를 구한 노드를 제외하고 남은 노드 중에서 이동 거리가 가장 짧은 노드를 선택합니다. 해당 노드는 최단 거리를 구한 노드로 설정합니다.
4) 선택한 노드의 인접 노드로 이동하는 간선의 가중치와 선택한 노드로 이동하는 이동거리의 합이 해당 인접 노드에 저장된 이동 거리를 비교하여 합이 작으면 바꿉니다.
5) 더 이상 선택할 노드가 없을 때까지 3 ~ 4번을 반복합니다.
2. 다익스트라 알고리즘 구현하기
인접 리스트를 이용한 다익스트라 알고리즘 구현
- 간선 단위로 처리를 수행합니다.
- 시간 복잡도 : O(NlogN) (N : 간선의 수)
코드는 다음과 같습니다.
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
/*
TC
5 8
0
0 1 6
0 2 5
0 4 1
1 2 5
1 4 3
2 4 9
2 3 4
3 4 10
*/
#define INF 0x7fffffff
typedef struct _adList {
int dest;
int value;
struct _adList* next;
}adList;
typedef struct _myHeap {
int vertax;
int distance;
}myHeap;
adList* node = NULL;
myHeap* heap = NULL;
int heap_size, * distance = NULL;
void _initDSA_(const int Vsize, const int Esize) {
node = (adList*)malloc(sizeof(adList) * Vsize);
heap = (myHeap*)malloc(sizeof(myHeap) * Esize);
distance = (int*)malloc(sizeof(int) * Vsize);
for (int i = 0; i < Vsize; i++) {
distance[i] = INF;
node[i].next = NULL;
}
heap[0].distance = INF;
}
//--- 인접리스트 구현하기 ---//
void add_adList(int s, int v, int value) {
adList* newEdge = (adList*)malloc(sizeof(adList));
adList* tmp = &node[s];
if (newEdge == NULL) {
printf("malloc eeror : newEdge\n");
exit(1);
}
newEdge->dest = v;
newEdge->value = value;
newEdge->next = NULL;
while (tmp->next != NULL) {
tmp = tmp->next;
}
tmp->next = newEdge;
}
//--- 최소힙 구현하기 ---//
void minHeapPush(myHeap data) {
heap_size += 1;
int child = heap_size;
int parent = heap_size / 2;
while (parent >= 1 && data.distance < heap[parent].distance) {
heap[child] = heap[parent];
child = parent;
parent = child / 2;
}
heap[child] = data;
}
myHeap minHeapPop() {
if (heap_size == 0) {
printf("heap is NULL\n");
exit(1);
}
myHeap result = heap[1];
myHeap newTop = heap[heap_size--];
int parent = 1;
int L_child = parent * 2 > heap_size ? 0 : parent * 2;
int R_child = parent * 2 + 1 > heap_size ? 0 : parent * 2 + 1;
while (parent < heap_size) {
int S_child = heap[L_child].distance < heap[R_child].distance ? L_child : R_child;
if (heap[S_child].distance < newTop.distance) {
heap[parent] = heap[S_child];
parent = S_child;
L_child = parent * 2 > heap_size ? 0 : parent * 2;
R_child = parent * 2 + 1 > heap_size ? 0 : parent * 2 + 1;
}
else
break;
}
heap[parent] = newTop;
return result;
}
int main(void) {
int Vsize, Esize, startPoint;
scanf("%d %d %d", &Vsize, &Esize, &startPoint);
_initDSA_(Vsize, Esize);
//--- 인접 리스트 구축 ---//
for (int i = 0; i < Esize; i++) {
int v1, v2, value;
scanf("%d %d %d", &v1, &v2, &value);
add_adList(v1, v2, value);
add_adList(v2, v1, value);
}
//--- 다익스트라 시작 ---//
distance[startPoint] = 0; //시작 지점을 초기화 및 힙에 삽입
minHeapPush((myHeap){ startPoint, distance[startPoint] });
while (heap_size >= 1) {
myHeap data = minHeapPop();
if (data.distance > distance[data.vertax])
continue;
adList* tmp = node[data.vertax].next;
while (tmp != NULL) {
if (distance[tmp->dest] > data.distance + tmp->value) {
distance[tmp->dest] = data.distance + tmp->value;
minHeapPush((myHeap) { tmp->dest, distance[tmp->dest] });
}
tmp = tmp->next;
}
}
printf("\nresult\n");
for (int i = 0; i < Vsize; i++) {
printf("%d to %d : %d\n", startPoint, i, distance[i]);
}
return 0;
}- 정보 : 다익스트라를 구현하는 시간보다 최소 힙과 인접 리스트를 구현하는데 시간이 더 걸렸습니다.
- 개인적으로 C보다는 C++를 추천합니다. C++ 에는 Vector, 인접 리스트, 우선순위 큐 등 자료구조를 라이브러리로 제공합니다.
인접 행렬을 이용한 다익스트라 알고리즘 구현
- 정점 단위로 처리를 수행합니다.
- 시간 복잡도 : O(N^2) (N : 정점의 수)
코드는 다음과 같습니다.
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
/*
TC
5 8
0
0 1 6
0 2 5
0 4 1
1 2 5
1 4 3
2 4 9
2 3 4
3 4 10
*/
#define INF 0x7fffffff
int** adMatrix = NULL; //인접 행렬
int* distance = NULL; //이동 비용
int* decision = NULL; //이동 비용확정 여부
int count_decision; //남은 비용확정 정점 개수
void _initDSA_(const int Vsize) {
adMatrix = (int**)malloc(sizeof(int) * Vsize);
if (adMatrix == NULL) {
printf("malloc error : adMatrix\n");
exit(1);
}
for (int i = 0; i < Vsize; i++) {
adMatrix[i] = (int*)calloc(Vsize, sizeof(int));
if (adMatrix[i] == NULL) {
printf("malloc error : adMatrix[%d]\n", i);
exit(1);
}
}
distance = (int*)malloc(sizeof(int) * Vsize);
decision = (int*)calloc(Vsize, sizeof(int));
if (distance == NULL || decision == NULL) {
printf("malloc error : distance or decision");
exit(1);
}
for (int i = 0; i < Vsize; i++)
distance[i] = INF;
count_decision = Vsize;
}
int main(void) {
int Vsize, Esize, startPoint;
scanf("%d %d %d", &Vsize, &Esize, &startPoint);
_initDSA_(Vsize);
//--- 인접 행렬 구축 ---//
for (int i = 0; i < Esize; i++) {
int v1, v2, value;
scanf("%d %d %d", &v1, &v2, &value);
adMatrix[v1][v2] = value;
adMatrix[v2][v1] = value;
}
//--- 다익스트라 시작 ---//
distance[startPoint] = 0;
decision[startPoint] = 1;
count_decision -= 1;
int node = startPoint;
while (count_decision > 0) {
printf("node : %d\n", node);
//--- distance 갱신 ---//
for (int i = 0; i < Vsize; i++) {
if (adMatrix[node][i] != 0 && decision[i] == 0) {
//인접 정점이면서 결정되지 않은 노드인 경우
if (distance[node] + adMatrix[node][i] < distance[i]) {
distance[i] = distance[node] + adMatrix[node][i];
}
}
}
//--- 미절된 노드 중에서 distance 최소 값 찾기 ---//
int min = INF;
for (int i = 0; i < Vsize; i++) {
if (distance[i] <= min && decision[i] == 0) {
min = distance[i];
node = i;
}
}
//--- 해당 노드는 비용확정 ---//
decision[node] = 1;
count_decision -= 1;
}
printf("\nresult\n");
for (int i = 0; i < Vsize; i++) {
printf("%d to %d : %d\n", startPoint, i, distance[i]);
}
return 0;
}- 확실히 인접 행렬은 구현하기 쉽습니다. (C기준)
'개념 정리 > 알고리즘' 카테고리의 다른 글
| 유클리드 호제법 | GCD, LCM (0) | 2021.12.21 |
|---|---|
| 두 포인터 알고리즘 (Two pointers method) (0) | 2021.06.28 |
| Greedy Algorithm (그리디, 탐욕 알고리즘) (0) | 2021.06.25 |
| Merge Sort (합병 정렬) (0) | 2021.06.23 |
| 크루스칼 알고리즘 & 프림 알고리즘 (0) | 2021.06.15 |

