1. 개념 정리
- 크루스칼 알고리즘(Kruskal's Algorithm)과 프림 알고리즘(Prim's Algorithm)은 그리디 알고리즘(Greedy Algorithm)을 적용한 것으로 무향 연결 그래프가 주어질 때 최소 스패닝 트리(Minimal spanning tree, 최소 신장 트리)를 찾아주는 알고리즘입니다.
*** 스패닝 트리(Spanning tree, 신장 트리) 정의 ***
- 연결 그래프의 부분 그래프로 모든 정점을 포함합니다.
- 트리의 성질을 따릅니다. (사이클이 없는 연결 그래프)
- n개의 정점이 있으면 n-1개의 간선이 존재하게 됩니다.
- 최소 스패닝 트리는 연결 그래프에서 나올 수 있는 스패닝 트리 중에서 간선들의 가중치 합이 가장 최소인 스패닝 트리를 의미합니다.

예시에서는 최소 스패닝 트리는 < 스패닝 트리 3 >이 되겠습니다.
2. 알고리즘 과정 및 구현
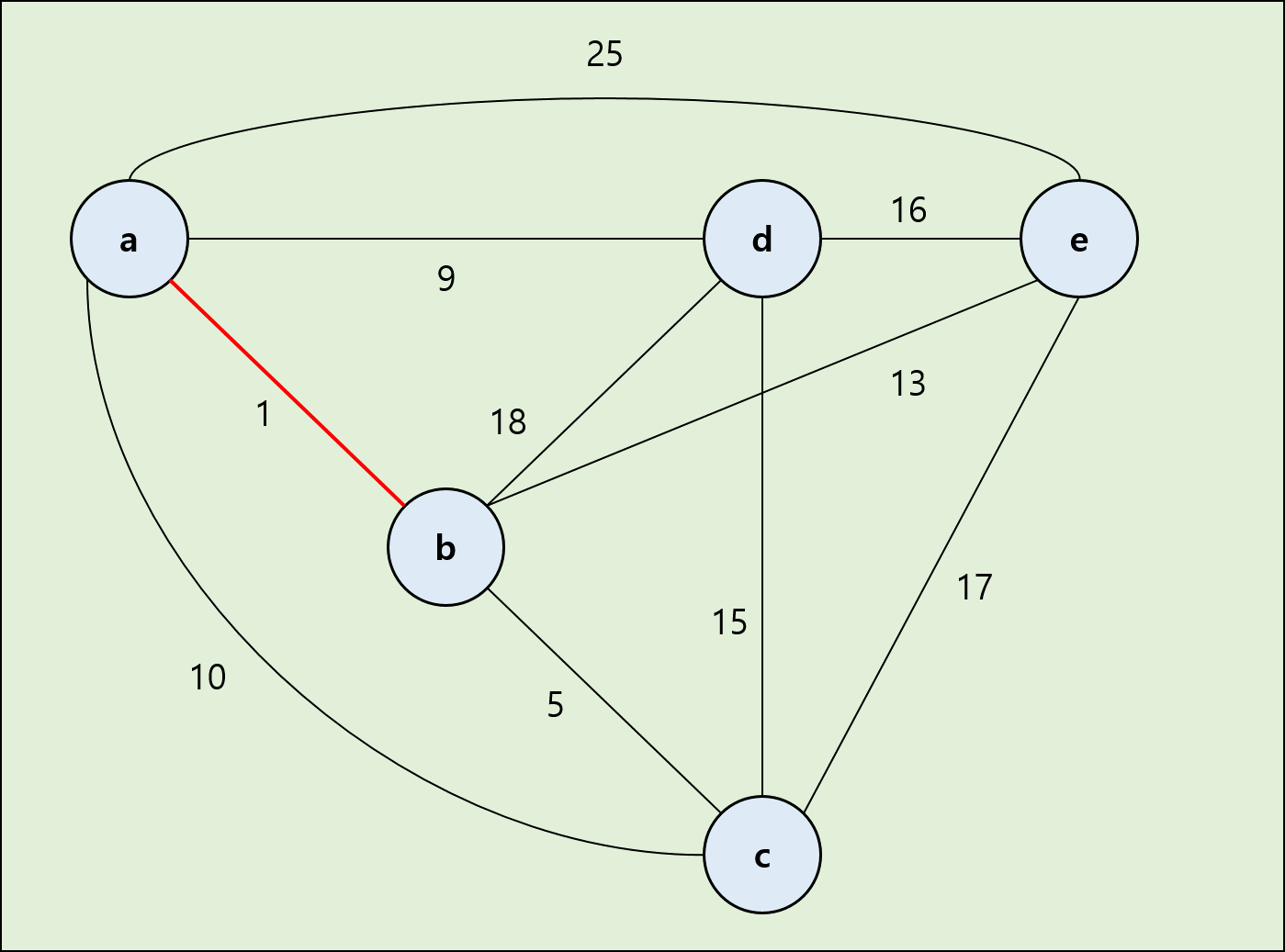
1) 크루스칼 알고리즘 (Kruskal's Algorithm)
과정 :
① 모든 간선들을 가중치에 따라서 오름차순으로 정렬합니다.
② 간선을 선택합니다. (단. 기존 선택된 간선들과 사이클 생길 경우에는 선택하지 않습니다.)
③ 2번 과정을 끝까지 반복하면 됩니다.










구현 :
#include<stdio.h>
#include<stdlib.h>
int main() {
int v_count = 1, e_count = 1;
int** map = NULL;
int* union_find = NULL;
scanf("%d %d", &v_count, &e_count);
union_find = (int*)malloc(sizeof(int) * v_count);
map = (int**)malloc(sizeof(int*) * e_count); //map[e_count]][3] : [x][0] -> vertex, [x][1] -> vertex, [x][y] -> value
//--- 동적할당 ---//
if (map == NULL || union_find == NULL) {
printf("heap malloc error\n");
exit(1);
}
for (int i = 0; i < e_count; i++)
{
map[i] = (int*)malloc(sizeof(int) * 3);
if (map[i] == NULL) {
printf("heap malloc error\n");
exit(1);
}
}
//--- 내용 초기화 ---//
for (int i = 0; i < e_count; i++) {
int s, e, v;
scanf("%d %d %d", &s, &e, &v);
map[i][0] = s;
map[i][1] = e;
map[i][2] = v;
}
for (int i = 0; i < v_count; i++) {
union_find[i] = i;
}
//--- 간선 정렬 (간단하게 버블 정렬 사용) ---//
for (int i = 0; i < e_count - 1; i++) {
for (int j = 0; j < e_count - i - 1; j++) {
if (map[j][2] > map[j + 1][2]) {
int tmp[3] = { map[j][0], map[j][1], map[j][2] };
map[j][0] = map[j + 1][0];
map[j][1] = map[j + 1][1];
map[j][2] = map[j + 1][2];
map[j + 1][0] = tmp[0];
map[j + 1][1] = tmp[1];
map[j + 1][2] = tmp[2];
}
}
}
//--- 간선 선택 ---//
printf("answer\n");
for (int i = 0; i < e_count; i++) {
if (union_find[map[i][0]] != union_find[map[i][1]]) {
printf("%d %d %d\n", map[i][0], map[i][1], map[i][2]);
int change = union_find[map[i][1]];
for (int j = 0; j < v_count; j++) {
if (union_find[j] == change) {
union_find[j] = union_find[map[i][0]];
}
}
}
}
}
여기서 간선을 정렬하는 알고리즘이랑 Union & Find 알고리즘을 좀 더 효율적으로 할 수 있습니다.
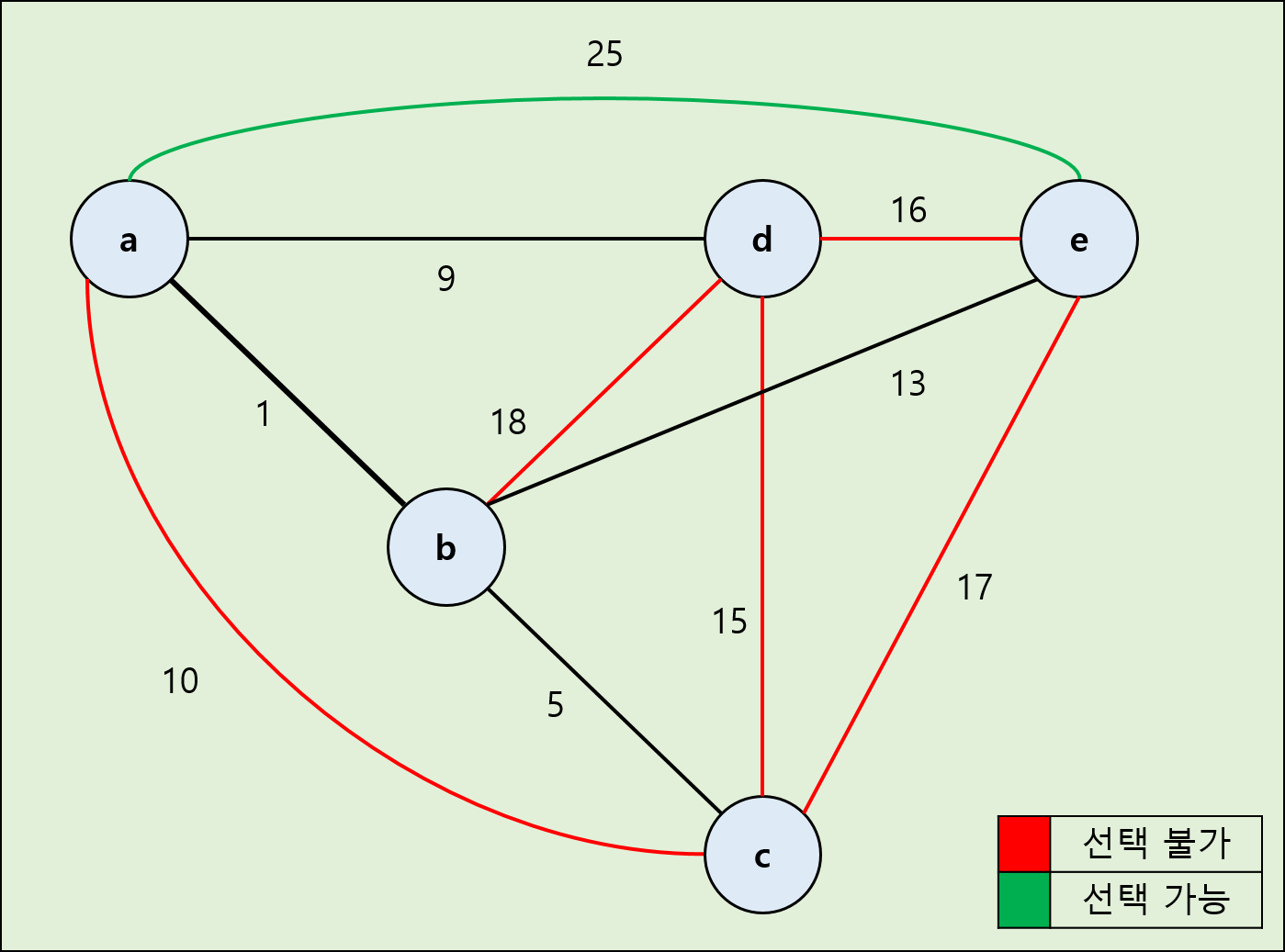
2) 프림 알고리즘 (Prim's Algorithm)
과정 :
① 가중치가 가장 작은 간선을 선택합니다.
② 선택한 간선들에 붙어있는 간선 중 가중치가 가장 작은 간선을 선택합니다. (단. 사이클이 생기는 간선은 선택하지 않습니다.)
③ 더 이상 선택할 수 있는 간선이 없을 때까지 2번을 반복합니다.
*다른 버전
① 임의의 정점을 선택합니다.
② 선택한 정점들에 연결된 간선 중에 가중치 가장 작은 간선에 연결된 정점을 선택합니다. (단. 이미 선택된 정점은 선택하지 않습니다.)
③ 더 이상 선택할 수 있는 정점이 없을 때까지 2번을 반복합니다.










구현 :
#include<stdio.h>
#include<stdlib.h>
#define MAX_VALUE 10000
typedef struct edgeStruct_ {
int vertex1;
int vertex2;
int value;
}edge;
void heap_insert(edge heap[], edge node, int* index) {
int parent = *index / 2;
int child = *index;
while (parent >= 1) {
if (heap[parent].value > node.value) {
heap[child] = heap[parent];
child = parent;
parent /= 2;
}
else
break;
}
heap[child] = node;
*index += 1;
}
edge heap_del(edge heap[], int* index) {
edge result = heap[1];
*index -= 1;
heap[1] = heap[*index];
int parent = 1;
while (parent < *index) {
int lchild = parent * 2;
int rchild = parent * 2 + 1;
int changenode = 0;
lchild = lchild >= *index ? 0 : lchild;
rchild = rchild >= *index ? 0 : rchild;
changenode = heap[lchild].value < heap[rchild].value ? lchild : rchild;
if (heap[parent].value > heap[changenode].value) {
edge tmp = heap[parent];
heap[parent] = heap[changenode];
heap[changenode] = tmp;
parent = changenode;
}
else
break;
}
return result;
}
int main() {
int v_count = 1, e_count = 1, index = 1;
edge min = {0, 0, 100};
edge* heap = NULL; //방문할 수 있는 간선
int** map = NULL; //정점과 정점간의 관계표현
int* is_contain = NULL; //정점 포함 여부
scanf_s("%d %d", &v_count, &e_count);
//--- 동적할당 ---//
is_contain = (int*)calloc(v_count, sizeof(int));
heap = (edge*)malloc(sizeof(edge) * e_count);
map = (int**)malloc(sizeof(int*) * v_count);
if (is_contain == NULL || heap == NULL || map == NULL) {
printf("heap malloc error!");
exit(1);
}
for (int i = 0; i < v_count; i++) {
map[i] = (int*)calloc(v_count, sizeof(int));
if (map[i] == NULL) {
printf("heap malloc error!!");
exit(1);
}
}
//--- 초기화 ---//
for (int i = 0; i < e_count; i++) {
edge tmp;
scanf_s("%d %d %d", &tmp.vertex1, &tmp.vertex2, &tmp.value);
map[tmp.vertex1][tmp.vertex2] = map[tmp.vertex2][tmp.vertex1] = tmp.value;
if (tmp.value < min.value) {
min = tmp;
}
}
heap[0].vertex1 = 0;
heap[0].vertex2 = 0;
heap[0].value = MAX_VALUE;
heap_insert(heap, min, &index);
map[min.vertex1][min.vertex2] = map[min.vertex2][min.vertex1] = 0;
//--- 간선 선택 ---//
printf("result\n");
while (index > 1) {
min = heap_del(heap, &index);
if (is_contain[min.vertex1] == is_contain[min.vertex2] && is_contain[min.vertex1] == 1) {
continue;
}
else {
printf("%d %d %d\n", min.vertex1, min.vertex2, min.value);
is_contain[min.vertex1] = is_contain[min.vertex2] = 1;
}
for (int i = 0; i < v_count; i++) {
edge node;
if (map[min.vertex1][i] != 0) {
node.vertex1 = min.vertex1;
node.vertex2 = i;
node.value = map[min.vertex1][i];
heap_insert(heap, node, &index);
map[min.vertex1][i] = map[i][min.vertex1] = 0;
}
if (map[min.vertex2][i] != 0) {
node.vertex1 = min.vertex2;
node.vertex2 = i;
node.value = map[min.vertex2][i];
heap_insert(heap, node, &index);
map[min.vertex2][i] = map[i][min.vertex2] = 0;
}
}
}
return 0;
}
마무리하면서 크루스칼이랑 프림의 결과가 다르게 나오는데도 동일하게 최소 스패닝 트리를 구한다는 그런 것을 보여주고 싶었는데 아무래도 예제를 잘 못 설정한 것 같습니다.
'개념 정리 > 알고리즘' 카테고리의 다른 글
| 두 포인터 알고리즘 (Two pointers method) (0) | 2021.06.28 |
|---|---|
| Greedy Algorithm (그리디, 탐욕 알고리즘) (0) | 2021.06.25 |
| Merge Sort (합병 정렬) (0) | 2021.06.23 |
| Quick Sort (퀵 소트) (0) | 2021.03.30 |
| Dynamic Programming : Knapsack Problem (0) | 2021.02.20 |


